01
勾股定理
内容：直角三角形两直角边的平方和等于斜边的平方；
表示办法：假如直角三角形的两直角边分别为a，b，斜边为c，那样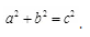
勾股定理的起源：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．国内古时候把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了勾三，股四，弦五形式的勾股定理，后来大家进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方
02
勾股定理的证明
勾股定理的证明办法不少，容易见到的是拼图的办法
用拼图的办法验证勾股定理的思路是
①图形进过割补拼接后，只须没重叠，没空隙，面积不会改变
②依据同一种图形的面积不一样的表示办法，列出等式，推导出勾股定理
容易见到办法如下：
办法1、
办法2、
四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角 
办法3、
化简得证。
03
勾股定理的适用范围
勾股定理揭示了直角三角形三条边之间所存在的数目关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具备这一特点，因而在应用勾股定理时，需要明了所考察的对象是直角三角形
04
勾股定理的应用
②了解直角三角形一边，可得另外两边之间的数目关系③可运用勾股定理解决一些实质问题
05
勾股定理的逆定理
假如三角形三边长a，b，c满足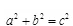
，那样这个三角形是直角三角形，其中c为斜边.
06
勾股数
07
勾股定理的应用
勾股定理可以帮助大家解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题．在用勾股定理时，需要把握直角三角形的首要条件条件，知道直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算，应设法添加辅助线（一般作垂线），架构直角三角形，以便正确用勾股定理进行求解。
08
勾股定理逆定理的应用
勾股定理的逆定理能帮助大家通过三角形三边之间的数目关系判断一个三角形是不是是直角三角形，在具体推算过程中，应用两短边的平方和与最长边的平方进行比较，切不可不加考虑的用两边的平方和与第三边的平方比较而得到错误的结论．
09
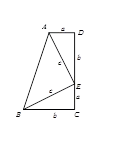
勾股定理及其逆定理的应用
勾股定理及其逆定理在解决一些实质问题或具体的几何问题中，是密不可分的一个整体．一般既要通过逆定理断定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决．容易见到图形：
